La spectrophotométrie permet d’étudier les propriétés de la matière et d’avoir accès à des informations sur le monde microscopique. En laboratoire, elle permet également de déterminer la composition et/ou la concentration d’un échantillon. La Loi de Beer-Lambert est l’un des outils permettant de mesurer la concentration d’un (ou plusieurs) composés en solution.
D’où vient la loi de Beer-Lambert ?
La loi dite de Beer-Lambert, parfois aussi appelée Loi de Beer-Lambert-Bouguer, a été établie suite aux travaux indépendants de trois savants : August Beer (1825-1863)[1], physicien, chimiste et mathématicien allemand originaire de Trèves (actuelle Allemagne), Jean-Henri Lambert (1728-1777)[2], mathématicien et philosophe né à Mulhouse (cité-Etat indépendante à cette époque) et Pierre Bouguer (1698-1758)[3], mathématicien et physicien français (né au Croisic). Tous les trois ont contribué à la compréhension du comportement de la lumière lorsqu’elle traverse des milieux non-transparents. Même si Beer, Lambert et Bouguer ont permis d’élaborer les équations décrivant ce phénomène, son explication, au niveau microscopique leur était inconnue ; elle n’a été proposée qu’au XXe siècle.
Quel est le principe de la loi de Beer-Lambert ?
Prenons un montage expérimental simple
(Fig. 1). Une source lumineuse (laser) émet un faisceau
lumineux caractérisé par une intensité I0,
qu’on appelle intensité incidente
(entrante). Ce faisceau lumineux passe à travers une cuve, et, en sortie du
montage, un détecteur est chargé de mesurer l’intensité du rayon sortant, qu’on
appelle l’intensité transmise (celle
qui passe) It. Le but est
de déterminer si toute ou seulement une partie de la lumière passe ou non,
en comparant l’intensité I0
entrante et l’intensité It
sortante (transmise).
Si It = I0, c’est-à-dire que l’intensité en sortie est la même que celle d’entrée, alors cela signifie que toute la lumière passe à travers la cuve (le milieu, l’échantillon) et on dit que 100 % de la lumière ont été transmis ou que 0 % a été absorbé (retenu, dévié, etc.). Dans ce cas, le milieu, l’échantillon ou la cuve sont dits transparents. Lorsque la lumière passe à travers un milieu quelconque (air, gaz, verre, liquide, etc.), on mesure souvent une intensité It (transmise) inférieure à l’intensité incidente I0, car il n’est pas transparent. On dit qu’une partie de la lumière a été absorbée par le milieu et donc que ce milieu est opaque ou absorbant.
On définit la transmittance T comme la fraction de lumière capable de traverser le milieu, c’est-à-dire comme le rapport entre l’intensité de lumière sortante (It) et l’intensité entrante (incidente, I0). Multipliée par 100, on mesure donc le pourcentage de lumière transmise, soit :
L’opacité (O) correspond à l’inverse de la transmittance (I0/It, et donc quantifie la capacité du milieu à empêcher la transmission de la lumière). Elle est beaucoup moins utilisée.
L’origine de l’absorption de la lumière
Lorsque qu’un faisceau de lumière traverse un milieu non transparent, son intensité diminue, et on mesure une intensité sortante plus faible. Cette « perte » d’intensité, l’absorption, peut avoir plusieurs origines qui sont bien connues aujourd’hui.
L’absorption des photons –
Les photons peuvent effectivement être absorbés par les électrons des molécules ou les atomes présents dans
le milieu traversé. Cette propriété, bien expliquée par la mécanique quantique,
tire son origine du fait que les électrons répartis autour des noyaux d’atomes,
ou encore ceux présents dans les liaisons covalentes, peuvent absorber un photon, acquérir l’énergie
qu’il transporte, et passer dans un état d’énergie plus élevé. Cette absorption
n’a lieu que si l’énergie du photon
incident (celui qui arrive) est au
moins égale à celle associée à l’orbitale de l’électron ; si ce n’est
pas le cas, l’électron n’absorbe pas le photon incident, et il peut continuer
sa course. Ainsi, si les photons incidents possèdent une énergie (voir Encart 1) telle qu’elle permet leur absorption par les
électrons présents à la surface d’un atome ou d’une molécule du milieu traversé,
et seulement dans ce cas, alors ils sont absorbés. Au niveau macroscopique de
l’expérience, le détecteur en sortie du montage détectera donc moins de
photons, et donc une intensité lumineuse plus faible. S’ils ne sont pas
absorbés, parce que les propriétés des molécules dans le milieu ne le
permettent pas, ou parce qu’ils ne possèdent pas l’énergie requise, alors il
n’y aura pas d’absorption.
La diffusion des photons – Un autre phénomène peut affecter les photons incidents lorsqu’ils traversent un milieu. Ils peuvent être diffusés (voir Encart 2). La diffusion désigne un phénomène physique pour lequel, lorsqu’un photon rencontre un atome, une molécule ou une particule plus grande (poussière, etc.), il peut entrer en collision avec eux et finalement être dévié de manière élastique (il rebondit) sans que ses propriétés ne soient altérées (longueur d’onde inchangée, etc.). Le résultat de cette collision élastique (diffusion) est que les photons changent de trajectoire. Donc, lorsqu’un faisceau lumineux traverse un milieu non transparent (contenant des atomes, des molécules ou autres), une partie des photons qui le constituent peuvent être dispersés (subir ce phénomène de diffusion) et être renvoyés dans toutes les directions. Comme le détecteur ne mesure que les photons dont la trajectoire est rectiligne (ceux qui traversent le milieu en ligne droite), alors il mesurera une quantité de photons sortants plus faible que ceux qui sont entrés, et donc une intensité transmise It plus faible que celle d’entrée I0. Les deux phénomènes (absorption et diffusion) peuvent se produire en même temps lorsque la lumière traverse un milieu (échantillon) et contribuer tous les deux à la diminution de la transmittance.
L’importance de la longueur d’onde
Comme nous venons de le voir, les photons peuvent être absorbés par les électrons lorsqu’ils possèdent une énergie suffisante pour provoquer un saut quantique, c’est-à-dire faire passer ces électrons d’un niveau d’énergie à un autre, plus élevé. Cela signifie que l’absorption ne se produit que si la longueur d’onde – et donc l’énergie (voir Encart 1) – des photons est adéquate. En d’autres termes, pour qu’un composé présent dans notre cuve (Fig. 1) ait un effet d’absorption, il faut que la longueur d’onde de la lumière soit telle qu’elle véhicule une énergie suffisante pour provoquer le saut quantique d’un ou plusieurs électrons présents dans l’atome ou la molécule qui le constituent. De plus, les liaisons covalentes, les doubles liaisons et les doublets non-liants des molécules, eux aussi constitués d’électrons, peuvent aussi absorber des photons. La longueur d’onde du photon nécessaire pour exciter ces électrons dépend du contexte dans lequel ils se trouvent.
 | |
| Figure 3 |
Prenons une molécule telle que le G-250, de la famille des triméthylméthanes qui est utilisée pour détecter les protéines dans la fameuse méthode de Bradford que tu as certainement déjà vue quelque part si tu es étudiant.e en biologie. Cette molécule possède plusieurs cycles phényles (Fig. 3) comportant des double-liaisons délocalisées, très riches en électrons, ainsi que plusieurs formes tautomériques (alternatives) différentes. Cela signifie que les électrons des double-liaisons peuvent se déplacer sur une grande surface. Pour ces raisons, le G-250, lorsqu’il est libre en solution, peut absorber les photons visibles (entre 400 et 800 nm). Si l’on prend le montage de la Fig. 1, on peut utiliser une source lumineuse (laser) pour laquelle on peut régler la longueur d’onde. Si, dans la cuve, on place une solution de G-250 à une concentration fixe, et qu’on éclaire l’échantillon avec ce laser, mais cette fois à plusieurs longueurs d’onde (la Fig. 3 en présente 27 différentes), on constate un phénomène intéressant. Le G-250 n’absorbe pas tous les types de photons, et, en plus, absorbe plus efficacement certains d’entre eux. Pour les longueurs d’onde proches de 800 nm (lumière rouge), on observe que la transmittance est quasiment de 100 %, ce qui signifie que la lumière passe quasiment intégralement à travers l’échantillon. Autrement dit, les photons possédant une longueur d’onde de 800 nm ne sont pas absorbés par le G-250. Plus on réduit la longueur d’onde, et plus la transmittance diminue, ce qui signifie que l’absorption des photons par le G-250 augmente, avec un maximum à 651 nm. Une fois cette longueur d’onde franchie, si l’on continue à diminuer l, la transmittance augmente à nouveau (l’absorption diminue), avec un minimum autour de 600 nm, puis, elle diminue (l’absorption augmente) à nouveau à mesure qu’on s’approche d’un nouveau pic d’absorption (transmittance la plus faible) vers 467 nm. Lorsque l diminue encore, l’absorption diminue à nouveau (la transmittance augmente). Ainsi, le G-250 peut absorber toute une gamme de photons de l différentes, mais il existe des l préférentielles, pour lesquelles l’absorption est maximale, centrées autour de 651 et 471 nm. Ce sont les longueurs d’ondes qui correspondent aux énergies les plus favorables pour que les photons incidents soient absorbés par les électrons du G-250.
Commentaire de la figure 3: La figure présente la molécule de G-250. La seconde partie présente le même montage qu'à la figure 1, dans 4 cas différents. Le même échantillon de G-250 en solution (liquide, donc) est éclairé par 4 lumières différentes, avec 4 longueurs d'onde différentes. Dans chaque cas, la lumière transmise est mesurée (transmittance et absorbance représentées). Si l'on effectue ce travail pour tout un tas de longueurs d'ondes différentes, on peut représenter l'absorbance (ou la transmittance) en fonction de la longueur d'onde, et obtenir ce qu'on appelle un spectre d'absorbance.
Note bien que la transmittance (la fraction de lumière qui a traversé l’échantillon) est maximale lorsque l’absorption est minimale. Il est par ailleurs nettement plus intuitif de raisonner en prenant en compte l’absorption, car c’est elle qui t’informe du fait que les photons sont effectivement absorbés. On peut alors utiliser l’opacité (l’inverse de la transmittance). L’opacité (O) augmente lorsque l’absorption par le composé augmente. Note bien que l’absorption des photons (et donc l’opacité ou la transmittance) par un composé dépend entièrement de la longueur d’onde de la lumière choisie. Donc, on mesure toujours la transmittance ou l’opacité à la longueur d’onde d’absorption maximale. On note donc toujours la transmittance et l’opacité avec, en indice, la longueur d’onde à laquelle l’expérience est effectuée (Tl, Ol). Dans notre cas, pour analyser, détecter ou doser le G-250, on utiliserait la longueur d’onde à 467 nm, qui correspond à l’absorbance maximale en lumière visible (ici jaune).
Bien entendu, il existe d’autres zones d’absorption dans les UV ou dans les infra-rouges, mais je ne les ai pas été représentées.
Pour résumer, la quantification de l’absorption de la lumière à une longueur d’onde donnée par un échantillon peut être faite grâce à la transmittance (Tl), l’opacité (Ol, l’inverse de la transmittance, 1/T) ou par l’absorbance (Al, qui est le logarithme décimal de l’opacité ou de l’inverse de la transmittance)
L’effet de la concentration et de l’épaisseur traversée
 |
| Figure 4 |
Lorsque la lumière traverse un milieu non vide, elle peut être diffusée ou absorbée par les composés qui s’y trouvent. La probabilité qu’elle subisse ces effets est d’autant plus grande que le nombre de composés présents dans le milieu est important ; cela implique que, plus la concentration d’un ou de plusieurs composés est élevée, plus ils occupent le volume de milieu, et plus la lumière sera diffusée et/ou absorbée, conduisant à l’atténuation du faisceau en sortie de montage. Donc, It est généralement d’autant plus faible – par rapport à I0 – que la concentration de composés est élevée. Inversement, plus la concentration de composé est faible, moins la lumière sera diffusée et/ou absorbée. C’est assez intuitif, finalement.
De même, pour une concentration de composé(s) fixe, si la distance que la lumière doit parcourir dans le milieu augmente, alors la probabilité qu’elle soit diffusée et/ou absorbée augmente, conduisant à une diminution de It par rapport à I0 ; inversement, si la distance à parcourir diminue, la probabilité de diffusion et/ou absorption diminue, ce qui impacte moins It. Une manière de formuler les choses est de dire que la transmittance diminue (la lumière passe moins) si la concentration augmente et si la distance à parcourir augmente. Autrement dit, La transmittance est inversement corrélée à la concentration et à la distance parcourue.
La question est maintenant de savoir si cette relation est linéaire ou non : Est-ce que la transmittance diminue proportionnellement avec l’augmentation de la concentration ou non ?
Commentaire de la figure 4: Effet de la concentration et de la distance parcourue sur la transmittance. Plus la concentration est élevée, plus la probabilité que les photons rencontrent un composé (molécules, etc.) et soient absorbés est grande. Donc l'absorbance augmente si la concentration augmente. De même, plus la distance est grande, et plus la probabilité d’absorption est grande. Si on augmente la longueur de l'échantillon, donc, l'absorbance sera plus grande. Le phénomène est similaire pour la diffusion.
Transmittance ou absorbance ?
Est-ce que la transmittance mesurée varie linéairement avec (proportionnellement à) la concentration ? Cette question peut paraître anodine, mais elle est en réalité importante dans un contexte expérimental, car il est beaucoup plus facile de travailler avec des relations linéaires qu’avec d’autres types de relations. Pour quelle raison ? Parce que, s’il existe une relation linéaire entre des quantités, on peut utiliser des règles de trois (produits en croix) pour les calculs, et, surtout, les représentations (des droites) sont facilement exploitables pour effectuer des extrapolations (prédictions).
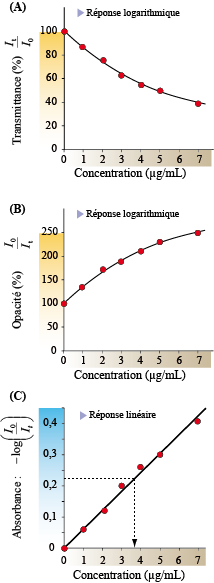 |
| Figure 5 |
De ce fait, –log(It/I0) est proportionnel à la concentration. Il existe entre eux une relation linéaire (Fig. 5C). Pour cette raison, c’est ce logarithme qu’on utilise. Il porte le nom d’absorbance. La Fig. 5C montre que l’absorbance augmente lorsque la concentration de l’échantillon augmente. Comme elle est linéaire (proportionnelle), cela signifie qu’une concentration deux fois plus élevée d’un composé aura une absorbance deux fois plus élevée ; autrement dit, doubler la concentration double l’absorbance, et ainsi de suite. L’absorbance est donc beaucoup plus intuitive à utiliser, et c’est la raison pour laquelle elle est largement répandue.
De manière générale, il y a une relation linéaire en l’absorbance, la distance parcourue par la lumière dans l’échantillon, et la concentration de l’échantillon.
Où Al est l’absorbance, c la concentration de l’échantillon et l la longueur parcourue par la lumière dans l’échantillon. Le facteur de proportionnalité el est le coefficient d’extinction ; el est spécifique à chaque composé. Il s’agit bien d’une équation de droite de type y = ax (où y = A, et où a= ell est une constante, puisque l est généralement fixe dans un appareil de mesure, et que el est fixe pour un composé donné ; où x=c, puisque c’est la concentration qu’on fait varier expérimentalement).
Quand peut-on utiliser la loi de Beer-Lambert ?
i) Le milieu constitué d’un composé absorbant la lumière ne doit pas être trop concentré. Pourquoi ? Parce que sinon, il est évident que toute la lumière pourra être soit diffusée, soit absorbée, soit les deux, à partir d'une certaine concentration: on ne mesurera alors plus rien et on n'obtiendra aucune information. La "concentration idéale" n'existe pas, et doit se déterminer expérimentalement. On verra ça une autre fois.
ii) Le composé à étudier ne doit pas réagir avec la lumière utilisée pour déterminer son absorbance. Autrement dit, il ne faut pas que le composé étudié change en interagissant avec la lumière, et, surtout, qu'il change d'une façon qui rend son absorption de la lumière différente !
iii) La lumière traversant le milieu doit être monochromatique, c’est-à-dire n’avoir qu’une seule longueur d’onde bien définie (notée l), ou, de manière équivalente, une fréquence unique (notée n, avec n = c/l, où c est la vitesse de la lumière dans le vide).
iv) le milieu doit être homogène (ses constituants doivent être distribués de manière homogène dans la solution ou le gaz, c’est-à-dire qu’ils soient distribués de la même manière dans tout le milieu).
Utiliser la Loi de Beer-Lambert
Les spectrophotomètres usuels disposent d’un laser émettant un rayon lumineux de longueur d’onde l contrôlée, d’intensité I0 connue, et d’un détecteur mesurant l’intensité transmise It, et ils donnent directement la valeur de l’absorbance Al (donc la valeur de –log(I0/It). Les cuves utilisées ont toutes une longueur l connue et standardisée (généralement 1 cm). Donc, avec cette valeur de Al, il est possible de déterminer la concentration d’un échantillon si l’on connaît le coefficient d’extinction el du composé analysé.
Si l’on mesure une absorbance donnée lors d’une expérience, comme :
Concentration vs. Quantité
La mesure de l’absorbance représente une information sur la concentration. C’est ce que dit la Loi de Beer-Lambert. On sait que la concentration est reliée à la quantité (molaire, n ou la masse m) par les relations suivantes :
La Loi de Beer-Lambert se formule de la manière suivante :
En prenant en compte les formulations de la concentration, et en remplaçant c par ces deux expressions, on obtient deux équations :
Que se passe-t-il si plusieurs composés sont présents en même temps dans le même échantillon ? On peut démontrer que les absorbances sont additives, ce qui signifie que chaque composé présent, s’il absorbe à la même longueur d’onde que les autres, contribue proportionnellement à sa concentration et à son coefficient d’extinction, à l’absorbance globale. On peut le formuler de la façon suivante : l’absorbance totale est la somme des absorbances individuelles, ou, mathématiquement :
Plus simplement: chaque composé qui absorbe apporte sa contribution à l'absorbance globale.Conclusion
Un de ces jours, je t'expliquerai comment on utilise la loi de Beer-Lambert dans des cas plus pratiques, ses limites, ses contraintes.
[1][1]Beer, A. (1852) Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten, Annalen der Physik und Chemie, vol. 86, p. 78-88.
[2] Lambert, J. H. (1760) Photometria, sive de mensura et gradibus luminis, colorum et umbrae, Sumptibus Vidae Eberhardi Klett, 1760.
[3] Bouguer, P. (1729), Essai d'optique sur la gradation de la lumière, Paris, Claude Jombert, p. 16-22.


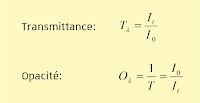










Aucun commentaire:
Enregistrer un commentaire